PENGENALAN SOFTWARE SPSS STATISTIK, NORMALITAS DAN TRANSFORMASI DATA ~ Syawal AFM

Penguasaan software statistik untuk memudahkan dalam pemaparan data terkait dengan data-data kesehatan masyarakat dan ini sangat diperlukan bagi Sarjana Kesehatan Masyarakat. Berbagai macam software statistik diantaranya adalah: SAS, SPSS, Stata, Epi Info, SUDAAN. S-PLIS, Statxact, BMDP, Statistica, Statview, program R dan lain-lain. Pada praktikum ini menggunakan software SPSS. Perlu diperhatikan sebelum mempraktekkan software statistik, praktikan harus mengikuti langkah-langkah dalam menggunakan uji statistik sebagai berikut:

1. merumuskan masalah

2. Menentukan hipotesis ( Ho dan Ha)

3. Design study

4. Mengumpulkan data

5. Interpretasi data

6. Menulis kesimpulan

1. Memasukkan data dan pengenalan SPSS

SPSS atau statistical packkage for sosial science, merupakan sebuah program aplikasi yang memiliki kemampuan analisa statistik cukup tinggi serta sistem pengoperasian cukup sederhana sehingga mudah dipahami. Terdapat dua langkah utama dalam memasukkan data yaitu mengisi variabel view dan data view.

ü Buka program SPSS

ü Aktifkan variabel view (kiri bawah)

Pada tampilan variabel view akan didapatkan kata name, type, widh, decimal,labels, vlues, column widh, aligment, measures. berikut ini adalah penjelasan dari masing-masing data isian tersebut.

Name Kata yang mewakili nama variabel. Biasanya disi dengan kata yang mudah diingat yang berkaitan dengan nama variabelnya, misalnya “sex” untuk variabel jenis kelamin responden.

Type tipe data yang dimasukkan. Pilihan yang paling umum adalah numeric (karena semua proses uji dalam SPSS bisa dilakukan dalam bentuk numeric) dan string ( kalau yang mau dimasukkan adalah huruf/kata/kalimat)

Width Jumlah digit data yang dimasukkan

Decimal Jumlah digit dibelakang titik

Labels penjelasan rinci dari kolom name. Misalnya, dalam kolom name di ketik sex, labelnya adalah “jenis kelamin responden”

Values kode yang diberikan jika variabel merupakan variabel kategorik (nominal dan ordinal).

Column width lebar kolom

Alignment pilihan tampilan variabel (rapat kiri, kanan, atau tengah)

Measures skala pengukuran variabel (nominal ordinal, scale). Dalam program SPSS, variabel interval dan rasio disebut varibel scale

Gambar 1. Isian variabel View

Tugas: masukkan data berat badan bayi dibawah ini dengan software SPSS

Tabel 1. Data berat badan bayi yang baru dilahirkan

No	Nama Ibu	Usia Ibu (Thn)	BB bayi (Kg)	jenis kelamin anak
1	Aminah	30	3	laki-laki
2	Shinta	23	2,3	laki-laki
3	Rutiami	22	2	laki-laki
4	Yuni	25	2,3	laki-laki
5	Bella	30	3	perempuan
6	Karni	20	2	perempuan
7	Nur azizah	32	2,9	perempuan
8	Siti Warliyah	24	2,4	perempuan
9	Hamidah	30	3	laki-laki
10	Hasminah	27	2,7	laki-laki
11	Amalia	24	2,4	laki-laki
12	Endang	29	2,9	perempuan
13	Tutik	28	2,6	perempuan
14	Imawati	32	3,1	perempuan
15	Irna	30	2,9	perempuan
16	Ekawati	24	2,3	laki-laki
17	Yanti	20	2	laki-laki
18	Asminah	25	2,5	perempuan
19	Nanik Sety	20	2	perempuan
20	Endang K	26	2,5	laki-laki
21	Ninin	32	2,8	laki-laki
22	Rondiyah	34	2,9	perempuan
23	Ekawarni	31	2,5	perempuan
24	Muspiah	25	2,6	laki-laki
25	Munawaroh	26	2,8	laki-laki
26	Sariyah	29	2,9	perempuan
27	Muslifah	20	3	perempuan
28	Karni	27	2,7	laki-laki
29	Suci	25	2,5	laki-laki
30	Murniati	24	2,4	perempuan

Cara kerja: terdapat dua langkah utama yang harus dilakukan, yaitu mengisi bagian variabel view dan mengisi data view.

ü Mengisi variabel view

Ø Buka program SPSS

Ø Aktifkan variabel view (ada di kiri bawah)

ü Mengisi data view

Klik data view, lalu isi sesuai data pada data kasus. Jika sudah sesuai simpan dengan nama: Latihan enty (fileè save asèlatihan entry) (simpan di folder d dengan nama dan NIM masing-masing mahasiswa) misal: Rano_06029032

Gambar 2. Data viev

2. Mengubah skala data variable

Tujuan: terampil melakukan perubahan data dari skala satu dengan skala yang lain. Misalnya dalam uji chi square diperlukan untuk melakukan perubahan skala numerik ke ordinal atau penggabungan sel (sebagai alternatif uji dalam chi square).

Cara kerja:

1. Buka file latihan

2. Aktifkan data view

3. Lakukan langkah-langkah berikut ini:

a. Transformèrecodeèrecode into diferent variabel

b. Masukkan vaiabel umur ke dalam input variabel

c. Ketik umur_1 ke dalam output variabel

d. Ketikkan klasifikasi umur kedalam label

e. Klik kotak change , setelah itu akan terlihat tampilan sebagai berikut:

f. Klik old and new values

g. Isilah kotak old value dan kotak new value (selanjutnya ikuti logika berpikir)

Gambar 3. Gambar tampilan Recode view

Logikanya:

Semua data <20 tahun diubah menjadi kode 1

Semua data 20-35 tahun diubah menjadi kode 2

Semua data >35 tahun diubah menjadi kode 3

Dengan logika tersebut, isilah old value dan new value sebagai berikut:

Old value: range lowest through 19, new value: 1, klik add

Old value: range 20 through 35, new value:2, klik add

Old Value: 36 trough higest, new value: 3, klik add

Pada tahapan ini akan diperoleh tampilan sebagai berikut:

Gambar 4. Tampilan Koding data

a. Proses telah selesai, klik kotak continu

b. Klik Ok

3. Membuat dan mendeskripsikan tabel frekwensi dan grafik untuk variabel kategori

Tujuan: menyajikan data supaya ringkas dan informatif sesuai dengan karakteristik data

Syarat tabel dan grafik yang baik: Ada Judul tabel atau grafik, Tahun pembuatan. Judul tabel dan grafik mencerminkan isi tabel, Ada sumber referensinya apabila tabel diambil dari data sekunder.

Cara kerja:

1. Buka file data Praktikum V

2. Klik Graphs==? Bar ( untuk grafik batang) atau line (untuk grafik garis)

3. Pilih simple dan summaries for groups of cases

4. Masukkan variabel area pada kotak category axix

5. klik ok

summaries of separate variabels: lakukan langkah-langkah berikut untuk memaparkan ringkasan grafis dengan pembandingan variabel yang ada pada data

a. klik graphsè bar (untuk grafik batang) atau line ( untuk grafik garis), maka kotak dialog bar charts atau kotak dialog line charts akan muncul

b. pilih clustered (untuk membuat grafik batang) atau pilih multiple (untuk membuat grafik garis), kemudian pilih summaries of separate variabels

c. klik define

d. masukkan variabel umur_ibu, berat_badan_bayi, hb, pendapatan pada kotak bar represent, kemudian masukkan variabel area ke kotak category axix

e. klik ok

Berkaitan dengan gambaran karakteristik data yang berskala kategori dikenal dengan istilah jumlah atau frekwensi tiap kategori dan prosentase tiap kategori yang umumnya disajikan dalam bentuk tabel atau grafik. Berikut adalah contoh penyajian data variabel kategori dalam bentuk tabel dan grafik batang.

Tabel 2.Distribusi Penderita Malaria Menurut Jenis Kelamin

di Kecamatan Kokap Kulonprogo 2015

No	Jenis Kelamin	Frekuensi	Persentase
1	Laki-laki	13	92,8
2	Perempuan	1	7,2
Jumlah		14	100

Sumber: Data Penelitian Solikhah 2009

Gambar 5. Distribusi Penderita Malaria Menurut Jenis Kelamin

di Kecamatan Kokap Kulonprogo 2009

1. Membuat dan mendeskripsikan variabel numerik

Tujuan: menyajikan data supaya ringkas dan informatif sesuai dengan karakteristik data

Cara kerja:

1. buka file data praktikum V

2. klik analysis=> deskriptive statisticsèfrequencies

3. masukkan variabel umur_ibu kedalam kotak variables

4. pilihan display frequency table di nonaktifkan

5. klik kotak statistic. Pilih mean, median, modus dapa central tendency (sebagai ukuran pemusatan), pilih Std deviation, variance, minimum, maksimum. Pada dispersion Pilih skewness dan kurtosis pada distribution (sebagai ukuran penyebaran)

6. klik continu, lalu aktifkan pilihann chart piliih histogram pada chart type dan aktifkan kotak with normal curve

7. klik continu, klik ok

Ada dua parameter yang lazim digunakan untuk mengambarkan karakteristik data dengan skala pengukuran numerik yaitu parameter ukuran pemusatan (tendency central) dan parameter ukuran penyebaran (dispertion). Parameter ukuran pemusatan yaitu, mean, median, dan modus. Untuk ukuran penyebaran, yaitu standar deviasi, varians, koefisien varians, interkuartil, range, dan nilai maksimum minimum. Data variabel dengan skala pengukuran numerik disajikan dalam bentuk tabel dan grafik (histogram dan plots).

Tabel 3. Contoh penyajian variabel numerik dalam bentuk tabel

Variabel	Rerata	Median	Simpang Baku	Minimum	Maksimum
Usia	46,69	47	12,56	15	69
Berat badan	50,4	50	8,33	45	64

Gambar 6. Contoh penyajian variabel numerik dalam bentuk histogram

Catatan: jika data mempunyai distribusi normal, dianjurkan untuk memilih nilai mean sebagai ukuran pemusatan dan standar deviasi sebagai ukuran penyebaran. Jika data berdistribusi data tidak normal, maka dianjurkan memilih nilai median sebagai ukuran pemusatan dan nilai maksimum minimum sebagai ukuran penyebaran.

A. TUJUAN PRAKTIKUM NORMALITAS DAN TRANSFORMASI DATA

1. Mahasiswa mampu melakukan dan menginterpretasikan sebaran dari data sampel

2. Mahasiswa mampu melakukan uji normalitas kolmogorov-Smirnov dan Shapiro-Wilk

3. Mahasiswa mampu melakukan penyajian data dari data yang telah diketahui sebarannya

4. Mahasiswa mampu melakukan transformasi data

DASAR TEORI

Pengetahuan dari sebaran data perlu diketahui untuk menentukan pemilihan dalam penyajian data dan uji hepotesis yang akan digunakan. Untuk penyajian data, apabila data terdistribusi norml maka dianjurkan menggunakan ukuran mean dan standar deviasi. Sedangkan untuk sebaran data tidak normal dianjurkan menggunakan median dan nilai maksmum dan minimum sebagai pasangan ukuran pemusatan dan penyebarannya. Sebaran data juga dapat digunakan untuk menentukan uji hipotesis yang akan digunakan. Uji parametrik digunakan apabila data terdistribusi normal, sedangkan uji non parametrik digunakan apabila sebaran data tidak normal. Terdapat dua metode untuk mengetahui set data memiliki ditribusi normal yaitu metode deskriptif dan metode analitik. Kedua metode tersebut dapat dilihat pada Tabel 4.

Tabel 4. Metode untuk mengetahui distribusi normal

Metode	Parameter	Nilai sebaran data (Normal)	Keterangan
Deskriptif (hitungan)	Koefesien varians (CoV)	Koefisien varian <30%	SD/Mean x 100%
	Rasio skewness (RS)	Nilai -2 s/d 2	Skewness/SE skewness
	Rasio kurtosis (RK)	Nilai -2 s/d 2	Kurtosis/SE kurtosis
Deskriptif (gambar)	Histogram	Simetris, tidak miring kiri/kanan, tidak terlalu tinggi atau rendah
	Box plot	Simetris, median tepat di tengah segi empat, tidak ada outlier atau nilai ekstrim
	Normal q-q plot	Data menyebar sekitar garis
	Detended q-q plot	Data menyebar sekitar garis
Analitik	Kolmogorov-Smirnov	p>0,05	Jumlah subjek >50
Analitik	Shapiro-Wilk	p>0,05	Jumlah subjek ≤50

UJI NORMALITAS DATA

Langkah-langkah:

1. Buka file : normalitas

2. Lihat variabel view

3. Liht data view

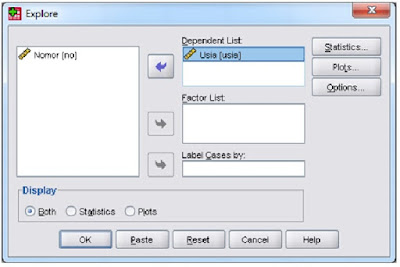
4. Analyze, Descriptive Statistic, Explore

5. Masukkan variabel usia ke dalam Dependent List

Akan terlihat tampilan sebagai berikut:

Gambar7. Tampilan perintah uji normalitas

1. Pilih Both pada Display

2. Biarkan kotak Statistics sesuai default SPSS. Pilihan ini akan memberikan Output deskrisi variabel

3. Aktifkan kotak Plots, aktifkan Factor level together pada Box plots (untuk menampilan box plot), aktifkan Histogram pada Descriptive (untuk menampilakn histogram), dan Normality plots with test (untuk menampilakn plot dan uji normalitas).

Akan terlihat tampilan sebagai berikut:

Gambar 8.Tampilan explore plot

1. Klik Continue, klik OK

Descriptives
			Statistic	Std. Error
Usia	Mean		39.8428	.33507
	95% Confidence Interval for Mean	Lower Bound	39.1834
	95% Confidence Interval for Mean	Upper Bound	40.5022
	5% Trimmed Mean		39.6436
	Median		39.0000
	Variance		33.569
	Std. Deviation		5.79389
	Minimum		25.00
	Maximum		60.00
	Range		35.00
	Interquartile Range		8.00
	Skewness		.569	.141
	Kurtosis		.429	.281

Interpretasi Hasil:

1. Menilai distribusi data secara deskriptif (menghitung dan melihat):

Dengan melihat output pada bagian Descriptives, marilah kita hitung beberapa parameter untuk menentukan normalitas distribusi data berdasarkan koefisien varian, rasio skewness dan rasio kurtosis.

a. Menghitung koefisien varian

Koefisien varian = (simpang baku/rerata) x 100% = (5,79/39,84) x 100% = 14,5%

b. Menghitung rasio skewness

Rasio skewness = Skewness/standar error of skewness = 0,569/0,141 = 4,04

c. Menghitung rasio kurtosis

Rasio kurtosis = kurtosis/standar error of kurtosis = 0,429/0,281 = 1,44

d. Melihat histogram

Dengan melihat histogram terlihat bahwa distribusi data cenderung miring ke kiri

e. Melihat Q-Q plot

Secara teoritis, suatu set data dikatakan mempunyai distribusi normal apabila data tersebar di sekitar garis.

Berdasarkan gambar diatas terlihat bahwa data menyebar disekitar garis, akan tetapi terdapat beberapa data yang letaknya jauh dari garis.

f. Melihat detended Q-Q plot

Secara teroritis, suatu set data dikatakan mempunyai distribusi normal apabila data tersebar di sekitar garis (angka nol).

Pada output diperoleh gambar terlihat bahw abanyak sekali data yang letaknya jauh dari garis

a. Melihat Box plot

Teori Boxplot

1) Kotak besar mengandung 50% data, yaitu persentil 25 sampai persentil 75. Garis tebal pada tengah kotak merupakan median (persentil 50). Wilayah ini dinamakan hspread.

2) Data 1,5 hspread dinamakan whisker.

3) Nilai lebih dari 1,5 hspread dinamakan data outlier

4) Nilai lebih dari 3 hspread dinamakan data ekstrem.

Secara teoritis suatu data dikatakan terdistribusi normal bila:

1) Nilai median ada di tengah-tengah kotak

2) Nilai whisker terbagi secara simetris ke atas dan ke bawah

3) Tidak ada nilai ekstrem atau outlier

Dari output, terlihat bahwa median terletak agak ke bawah kotak, nilai whisker relative simetris, terdapat data outlier. Jadi sebaran datanya tidak normal

1. Menilai distribusi data secara analitis

Tests of Normality
	Kolmogorov-Smirnov^a			Shapiro-Wilk
	Statistic	Df	Sig.	Statistic	Df	Sig.
Usia	.108	299	.000	.975	299	.000
a. Lilliefors Significance Correction

Untuk mengetahui data terdistribusi normal atau tidak secara analitis, bisa menggunakan uji Kolmogorov-Smirnov atau Shapiro-Wilk.

Pada uji normalitas, diperoleh p<0,001. Karena nilai p<0,05 maka bisa diambil kesimpulan bahwa distribusi umur tidak normal.

TRANSFORMASI DATA

Manfaat: terampil melakukan transformasi data untuk menormalkan distribusi data yang tidak normal. Langkah ini adalah salah satu langkah penting untuk menentukan uji hipotesis yang dipilih.

Kasus: Penelitian mengukur densitas parasit pada pasien malaria. Peneliti menguji normalitas data dan memperoleh bahwa data densitas parasit berdistribusi tidak normal.

Selanjutnya, peneliti mencoba untuk menormalkan data dengan menggunakan fungsi log 10

Langkah-langkah:

a. Buka file: transform_rerata geometrik

b. Klik Transform, Compute

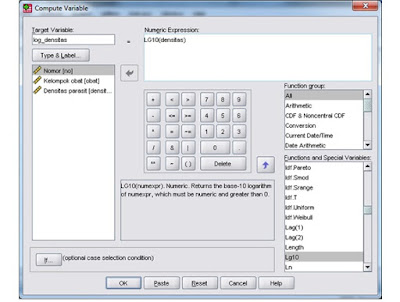
c. Ketik log_densitas ke dalam kotak Target Variable

d. Cari pilihan LG10 pada pilihan Fuctions, kalau sudah ditemukan pindahkan ke kotak Numeric Expression dengan mengklik tanda panah. Terlihat ada spasi setelah kata LG10 (?

e. Pindahkan variabel densitas ke spasi tersebut dengan mengklik tanda panah. Terlihat variabel densitas mengisi spasi yang kosong tadi.

Gambar 9. Tampilan compute variabel

f. Klik OK

Lihat pada data view. Pada data view terdapat variabel baru bernama log_densitas yang merupakan hasil dari transformasi variabel densitas parasit.

Tugas: lakukan uji normalitas untuk variabel log_densitas dengan langkah-langkah uji normalitas yang telah di bahas

Daftar Pustaka

1. Dahlan M.Sopiyudin, 2012, Statistika untuk Kedokteran dan Kesehatan, Penerbit Salemba Medika, Jakarta.

2. Dahlan M.Sopiyudin, 2014, Deskriptif, Bivariat dan Multivariat dilengkapi dengan Aplikasi SPSS Edisi 6, Penerbit Epidemiologi Indonesia, Jakarta.

3. Dergibson Siagian & Sugiarto. Metode Statistika untuk Bisnis dan Ekonomi, halaman 4-6". 2002. Jakarta : PT Gramedia Pustaka Utama. ISBN 979-655-924-2

4. Bernard Rosner; Fundamental of Biostatistics (Fith Edition): Hardvard University, Thomson Learning.

5. Budiarto Eko, 2001, Biostatistika untuk kedokteran dan kesehatan Masyarakat, EGC, Jakarta.

6. Chandra Budiman, 1995, Pengantar Statistik Kesehatan, EGC, Jakarta

7. Ritonga A, 1987, Statistika Terapan Untuk Penelitian, Lembaga Penerbit FE UI.Supranto J, 2001, Statistik Teori dan Aplikasi Jilid 2, Penerbit Erlangga, Jakarta.

8. Jay S.Kim and Ronald J. Dailey, 2008, Biostatistics for oral Healh Care, Blackwell Munkgaard, California

Syawal AFM

PENGENALAN SOFTWARE SPSS STATISTIK, NORMALITAS DAN TRANSFORMASI DATA

1 comment:

Cari Blog Ini

Report Abuse

Labels

Blog Archive

BTemplates.com

Labels

Blogroll

About